In the first chapter we studied about whole numbers. We learned about basic roman numerals, number order and structure, fractions, decimals, percentage, and reviewing on last year lesson.
Roman Numerals
- 1 = I
- 2 = II
- 3 = III
- 4 = IV
- 5 = V
- 6 = VI
- 7 = VII
- 8 = VIII
- 9 = XI
- 10 = X
*I as in 1 for Roman Numerals can only be used 3 times in a numerals. For example is when we write 4, for 4 we use subtraction (-) not addition (+) so it will be IV (5-1) instead of IIII (1+1+1+1)
Fractions
In fraction we learned about how to add, subtract, multiply, and divide fractions. We also learned to change fraction into mix numbers and vice versa.
In fraction we learned about how to add, subtract, multiply, and divide fractions. We also learned to change fraction into mix numbers and vice versa.
To add and subtract fraction we firstly need to match the denominator so that it will be the same number. After that will be the same as normal subtraction.
*The way to match the denominator is by finding the lowest common multiple of both denominator. Then divide the LCM with the denominators and multiply it with the existing numerator to get the new numerator.

This process is only used for fractions with different denominator. However if the denominators are the same just do it like normally. Example below.

To multiply fractions just multiply the numerator with the other numerator and denominator with the other denominator.

*The process in which you simplify the fractions you are multiplying by dividing either the first fraction's numerator with the second fraction's denominator or vice versa is called cancelation.
To divide a fractions you just need to make one of the fraction reversed or upside down then change it into multiplication. After that multiply and simplify them.
Examples below:
Decimals
In decimals, we learned about adding, subtracting, multiplying, and dividing decimals. We also learned about converting decimals to fraction or percentage.
In decimals, we learned about adding, subtracting, multiplying, and dividing decimals. We also learned about converting decimals to fraction or percentage.
To add and subtract decimals we can just do it directly like usual. But pay attention to the dot because they should be on top of each other.
To multiply decimals we need to see the numbers behind the dots. But first forget about the decimal. points/ dots,If the sum of numbers in both or all decimals is 3 digits so later move the dot 3 times.

To divide decimals we need to make all decimals become whole numbers. we can do it by multiplying them with 10, 100, 1000, 10000, 100000, and so on as long as it is the multiple of 10. However, don't forget if one decimal is multiplied the other decimal must also be multiplied so that they will be balanced.
To convert decimal to fractions you need to see how many digits behind the dots.
1 = /10
2 = /100
3 =/1000
To convert decimal to percentage just multiply them by 100%.
Percentage
To convert percentage to decimals, we need to divide them with 100 %. So they will be a decimal.

To convert percentage to fraction we need to make it become over 100 (/100) then simplify.
To find a percentage of a quantity we need to multiply the quantity with the percentage over 100. Like this:
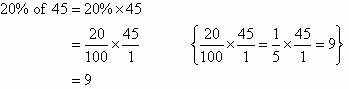
Work Example from our book:
Ratio
In ratio, we learned about how to use ratio for word problems. We also learned equivalent ratio, and dividing a quantity with a given ratio.
First of all, ratio can be expressed by :(double dots or colon), / and "to"
In using ratio to solve word problem, we must know the question and understand them. First, we need to find 1 first. After that, we just need to multiply the 1 with each given ratio.
For equivalent ratio, we can multiply both or more numbers with the same numbers. You can also simplify them by dividing them with the same number.
For dividing a quantity with the given ratio, this concept is related with the first concept. We can find I first.
These are several questions and its solution:
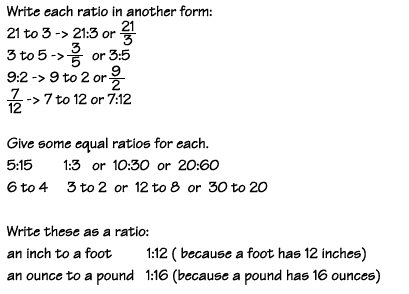

Rates
In rates we learned about distances, time, simplifying rate, writing numbers as rate, and many more. Here you will see examples, solution, and the how it works.
Observe this as an example:
Write each of the following as a rate in simplest form.
8 KM in 2h
To write this as a rate we need to use the symbol / or per.
It will become
8 Km/2H
But in rate you must make it as simplest form
So it will become
4km/h
This just one example of rate that I have learned.
Scale Drawing
In scale drawing, we still apply the concept of ratio. Scale drawing of an object is the same shape as the object but a different size.
Scale = length on drawing : real length
A scale can be written in two ways, as 1 cm: 1 m or 1cm :100cm (1m)
If the scale drawing is larger than the real length, then the scale drawing is called anenlargement and the first term of the scale would be the larger.
For example:
A real distance of a line 10 m. But the scale drawing is only 5 m.
It should be 5 : 10 but its not the simplest form so you must simplify them become 1m for the scale per 2m for the real distance.





No comments:
Post a Comment